Algorithmen
Programmiersprachen
Tipps und Tricks
|
Konstruktion eines Spektrums aus RGB-Werten
Die Problematik
Wie in Farbensehen gezeigt ist, ist es nicht möglich
aus nur drei Werten (RGB) wieder ein Spektrum zu gewinnen. Auch wenn dieses nicht
kontinuierlich sondern aus diskreten Wellenlägen bestehen soll.
Da verschiedene Spektren zu den selben RGB-Werten führen. Die Rekonstruktion
kann daher nicht mehr eindeutig sein.
Was wir wollen ist dann also ein mögliches plausibles
Spektrum, was im Bild natürlich aussieht und für die meisten Fälle gut "passt".
Abbildung 1 zeigt zwei grundverschieden Spektren, die beide zum RGB-Wert "weiß",
also zum Beispiel (255, 255, 255) führen.

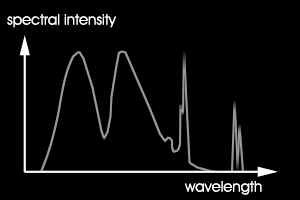
Abb.1 zwei Spektren die beide weiß ergeben (schematisch)
links: gleichmässiges kontinuierliches Spektrum
rechts: Spektrum eines "Weiss" auf dem Bildschirm
Für unsere Belange wird das kontinuierlich Spektrum links geeigneter sein als ein
Spektrum aus drei sehr schmalbandigen Peaks.
Dagegen kann ist für reines Rot (255, 0, 0) ein sehr begrenztes Spektrum nötig.
Denn nur so sind keine Anteile für Grün und Blau enthalten.
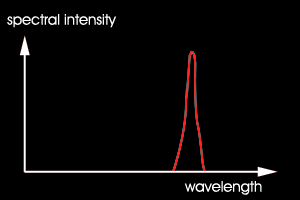
Abb.2 ein mögliches Spektren für reines Rot (schematisch)
Für die anderen zwei Farbwerte gilt das natürlich analog.
Aber was macht man mit anderen Farben als diesen extremen reinen Farben (Rot, Grün, Blau, Schwarz, Weiß und Grau)?
Z.B. ein Rosa (255, 200, 200)? Mathematisch korrekt könnte man eine Kombination aus
einem kontinuierlichem gleichmäßigen weißanteil und einem reinen Rot wie dem oben basteln.
Das resultierende Spektrum ist in Abb. 3 links dargestellt.
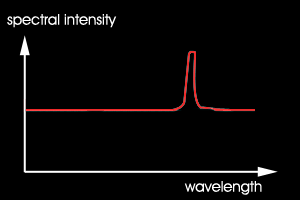
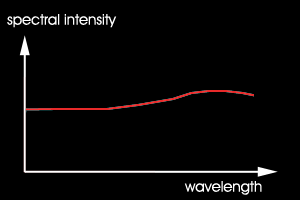
Abb.3 theoretisch mögliches Spektrum für rosa
links: als Linearkombination von kontinuierlichem Weiss und reinem Rot
rechts: als möglichst glattes Spektrum
Aber hätte ein natürliches Rosa nicht eher ein Spektrum wie Abb. 3b?
Und was ist mit Mischfarbe wie Gelb, Cyan und Violett? Ein Kombination aus Rot, Grün und Blau
erscheint nicht sinnvoll. Denn ein Gelbes Spektrum sollte auch das Maximum im Gelben Spektralbereich
haben usw.
Die gewünschten Eigenschaften eines solchen Spektrums
Spektrales Maximum
Bis auf den Sonderfalls der im realen Spektrum nicht vorkommenden Magenta-Farben sollte das Maximum
eines Spektrums dort sein wo auch die entsprechende Spektralfarbe liegt. D.h. en gelblicher RGB-Farbwert
sollte zu einem Spektrum führen welches im gelben Bereich sein Maximum hat. EInSpektrum einer unbunten, grauen
Farbe sollte über den gesamten Wellenlängenbereich konstant sein.
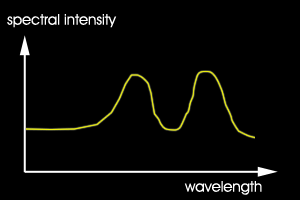
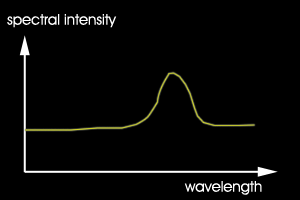
Abb.4 konstruiertes Spektrum für einen blassen gelben Farbwert
links: als Kombination eines grünen und roten Ausgangsspektrums
rechts: als Spektrum mit Maximum im gelben Bereich
Glattheit
Das Spektrum sollte möglichs glatt sein. Also möglichst flachen Anstiege aufweisen
mit ebenso wenigen "Dellen" und einem sanften Maximum.
Der Übergang von reinen Spektralfarben zu Unbunttönen sollte kontinuierlich verlaufen wobei
mit größerer Sättigung die Breite des Maximums abnimmt.
Ähnliche Farben - ähnliche Spektren
Ähnliche RGB - Farbwerte sollten zu ähnlichen Spektren führen.
Was gar nicht geht kann
Quecksilberdampflampen haben mehrere scharfe Spektralinien. Zusammen ergeben sie ein
grünlich-weißes Licht. Die Spektralrekonstruktion wird daraus dann ein weisses kontinuierliches
Spektrum mit einem Maximum im grünen Wellenlängenbereich. Das entspricht aber nicht der Realität.
Aber leider kann man es prinzipiell nicht von einem grünlichen Weiß unterscheiden.
Geht halt nicht anders ohne eine komplizierte Unterscheidung und eine Art Spektralbibliothe natürlicher
Farben einzuführen.
mathematische Konstruktion eines Spektrums aus RGB
Diskretes Spektrum
Um in endlicher Zeit rechnen zu können, brauchen wir natürlich ein diskretes Spektrum und kein wirklich
kontinuierliches. Die Frage ist, welche Auflösung sollte ein Spektrum haben. Wieviel Wellenlägen sollen
wir betrachten?
Die Frage lässt sich recht einfach beantworten: genau so viele wie man benötigt!
Und wieviel benötigt man nun? Will man das Spektrum über hundert Pixel darstellen, braucht man
ohne weiter Interpolationen hundert Wellenlängen. D.h. je weniger das Spektrum in der Darstellung gestreckt
wird, desto weniger Stützstellen braucht man. Wird das Spektrum eine Pixels auf einen Pixel abgebildet, kann
man gleich mit den origialen RGB-Werten arbeiten. Aber auch nach oben hin ist die sinnvolle Anzahl begrenzt.
Je größer die Auflösung ist, desto geringer ist der Anteil der einzelnen Spektrallinien.
Liegt der Anteil unter der Auflösung der Farbkanäle, also meist 1 / 255, dann bemerkt man die höhere Auflösung
nicht mehr. Und im Gegenteil, durch die geringeren Zahlenwerte kann es zu größeren numerischen Fehlern kommen.
Erst recht wenn man mit Integerwerten arbeitet. Und natürlich steigt die Rechenzeit proportional zur Anzahl der
Wellenlängen. Mehr spektrale Stützwerte als 200 sind demzufolge kaum sinnvoll.
Colormatching Funktionen und Darstellung des Spektrums
Für jedes Tripel von Primärvalenzen, ob das nun RGB eines Bildschirms oder CIE XYZ oder sonstwas ist,
lassen sich sogenannte Colormatching Funktionen ermitteln.
Die Colormatching Funktionen beschreiben, welches Werte man für die gewählten
Primärvalenzen angeben muss, um den gleichen Farbeindruck (also metamere Farbgleichheit) zu bekommen
wie eine bestimmte reine Spektralfarbe, welche durch die Wellenlänge gegeben ist.
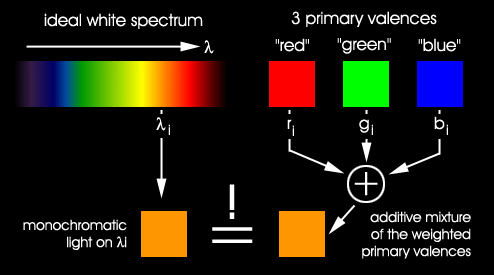
Abb.5 Bestimmung der colormatching functions
Die Idee ist, dass man sich eine (nahezu) monochromatische Farbe aus dem Lichtspektrum anschaut und
dann durch Einstellen der Anteile der gewählten Primärvalenzen versucht,
diesen Farbeindruck als additive Mischung dieser Primärvalenzen einzustellen.
Angenommen man wählt als Primärvalenzen die üblichen Bildschirmphosphore dann erhält man
für eine bestimmte Wellenlänge li beispielsweise
die Werte ri, gi, bi. Das heißt (ri, gi, bi)
ist der RGB-Wert, den man einstellen müsste um den Farbeindruck der reine Spektralfarbe der Wellenlänge li
auf dem Bildschirm nachzubilden. Geht man durch das gesamte sichtbare Spektrum, erhält man so die drei
Colormatching Funktionen mR(l), mG(l), mB(l).
Zu bachten ist allerdings, dass diese Funktionen negativ werden können und müssen!
Die negativen Anteile resultieren aus der Tatsache, dass es bekanntlich nicht gelingt mit nur drei
Primärvalenzen den gesamte sichtbaren Farbraum, insbesondere die reinen Farben des Spektrums, nachzubilden.
Um das zumindest rechnerisch zu ermöglichen, haben alle Colormatching-Funktionen (deren Primärvalenzen innerhalb
des sichtbaren Farbraumes liegen) eben negative Anteile. (Nur am Rande: Die Colormatching-Funktionen der theoretischen
CIE-XYZ-Farbvalenzen haben demzufolge nur postive Anteile.)
Die negativen Anteile kann man im Experiment durch hinzufügen eines Weiß-Offsets simulieren oder man
ermittelt sie rein rechnerisch.
Für unsere Zwecke benötigen wir die Colormatching-Funktion für den üblichen RGB-Farbraum.
Es ist dabei egal, ob RGB, sRGB, NTSC etc. Die Unterschiede sind zu gering als dass sie ins Gewicht fallen.
Für jede Wellenlänge li kennen wir nun also über die
Colormatching Funktion die RGB Werte ri, gi, bi, die wir wählen müssen um diese Wellenlänge korrekt
am Bildschirm darzustellen:
ri = mR(li) = mR(i)
gi = mG(li) = mG(i)
bi = mB(li) = mB(i)
Statt mit der konkreten Wellenlänge li können wir im folgenden einfach nur
den Index i benutzen, da wir es mit einem disktreten Spektrum zu tun haben und die konkreten Wellenlängen nicht
interessieren.
Selbstverständlich müssen zur Darstellung auf dem Bildschirm eventuelle negative Werte zu 0 und
zu große Werte auf 1.0 (bzw. 255) geclippt werden. Aber natürlich erst nach der Berechnung.
Die Colormatching-Funktionen müssen aber noch eine andere Bedingung erfüllen. Und zwar muss das Integral über die
Wellenlänge - also die Summe, da wir mit einen diskreten Spektrum rechnen - 1.0 ergeben! Denn nur so ist eine
transparente Konvertierung RGB->Spektrum->RGB möglich.
∑ mR(i) = 1.0 (bzw. 255) !
∑ mG(i) = 1.0 (bzw. 255) !
∑ mB(i) = 1.0 (bzw. 255) !
scheinbare Unnatürlichkeit vs. schönes Spektrum
Ein solches weisses Spektrum (Abb. 6 oben) sieht lieder auf dem ersten Blick nicht so aus wie man es erwarten würde.
So scheinen die Farben Blau, Grün und Rot zu domieren. Das helle Gelb fehlt und auch Cyan ist sehr dunkel.
Violette verschwindet im schwarz und rechts neben dem Rot ist auch viel schwarz.
Ein Spektrum sollte doch so aussehen, wie auf Abb. 6 unten aussehen...

Abb.6 schönes vs. farbmetrisch "richtiges" Spektrum
Dazu findet man unter anderem hier weiter gehende Information:
http://www.itp.uni-hannover.de/~zawischa/ITP/sonnspekt.html.
Der Effekt ist unter "Bezold-Brücke-Effekt" bekannt "Der Farbton eines Reizes hängt nicht nur von dessen relativer spektraler Zusammensetzung ab,
sondern auch von der Intensität". Desweiteren spielt auch die Einteilung der Abszisse. Sind die Wellenlängen
linear oder logarithmisch angeordnet? Beugungsspektrum oder Brechungspektrum?
Der schwarze rechte Rand ist übringes dunkels Rot, da unsere Empindlichkeit zum Infraroten nur sehr
langsam abnimmt. Der rote Laser des CD-Players ist eigentlich schon (fast) Infrarot. Eigentlich sieht
man ein so langwelliges Rot kaum noch. Das man trotzdem was sieht ist der hohen Intensität zu verdanken, die
man deswegen nicht unterschätzen darf!
Die benutzen Colormatchingfunktionen berücksichtigen auch diesen Bereich.
Ich habe mich entschlossen, mit den farbmetrisch bestimmten Spektrum zu arbeiten.
Man könnte sich aber vorstellen die RGB-Werte des "schönen" Spektrums zu nehmen.
Dann erhält man andere Colormatching-Funktionen und kann verfahren wie beschrieben.
Allerdings sind es dann keine Colormatching-Funktionen mehr.
Konstruktion des Spektrum
Ein diskretes Spektrum kann man beschreiben mir den spektralen Intensitäten si(li) für
alle i (i = 0...n-1 bei n diskreten Wellenlängen)
Das Spektrum kann dann mit den Colormatching Funktionen dargestellt werden. Dabei
werden diese Werte mit den normierten spektralen Intensitäten multiplziert.
ri = mR(i) ⋅ si
gi = mG(i) ⋅ si
bi = mB(i) ⋅ si
Um die ursprünglichen RGB-Werte zu erhalten muss man nur ri, gi und bi
über alle Wellenlängen integrieren...pardon...summieren:
R = ∑ mR(i) ⋅ si
G = ∑ mG(i) ⋅ si
B = ∑ mB(i) ⋅ si
Diese drei Gleichungen sind dann im Grunde schon das Gleichungssystem um aus R, G, B und
den Colormatching-Funktionen das Spektrum, also alle si zu ermitteln.
Dummerweise ist es "leicht" unterbestimmt...n Unbekannte aber nur 3 Gleichungen.
Unter berücksichtung der Punkte aus Die gewünschten Eigenschaften eines solchen Spektrums
kann man nun die verschiedensten mathematischen Ansätze verwirklichen um das Spektrum zu bestimmen.
Oder man macht es per Hand...das geht recht gut, wenn man sich ein Programm mit GUI
schreibt und die Kurven mit der Maus malen kann. Gegebenfalls können Zwischenwerte z.B. per
Spline-Interpolation interpoliert werden. Um ehrlich zu sein, die manuelle Methode brachte
die besten Ergebnisse.
Der Algorithmus
schnelle Linearkombination aus Grundspektren
Welchen Algorithmus man auch wählt um aus RGB-Werten eine Spektrum zu erstellen,
er sollte eine Eigenschaft haben: schnell sein.
Schon deshalb fällt eine auswändige mathematische Bestimmung mit Lösen von Gleichungssystemen
und interativen Verfahren aus.
Ein Lookup-Table für alle RGB-Werte wird zu groß werden. Aber wenn man die Lookuptabelle
klein macht? Und Zwischenwerte interpoliert?
Dann ist man bei einer Linearkombination wie sie in Abb 3. schon angedeutet wurde.
Nur genügt es eben nicht, nur ein paar Grundfarben Rot (1.0, 0.0, 0.0), Grün(0.0, 1.0, 0.0), etc.
und Weiss zu nehmen. Sondern man braucht einige mehr.
Es sei m die Anzahl der Spektren, die als Lookuptable vorgehalten werden. Dazu kommt noch der weiss-Anteil,
der aber trivial einfach nach Bedarf dazu addiert werden kann.
Für die m Spektren Sj (j = 0 ... m-1) sind die einzelnen Spektralen Intensitäten mit
irgendeinen geeigneten Verfahren bestimmt wurden und liegen dann als je n Werte sji in der Lookuptable vor.
Jedes dieser m Spektren repräsentiert genau einen RGB-Wert (Rj, Gj, Bj).
Die Aufgabe des Algorithmus besteht jetzt lediglich aus dem Set der m Teilspektren welche jeweils einen RGB-Wert
repräsentieren, einige wenige geeignete auszuwählen und die Faktoren zu bestimmen mit denen sie addiert werden, so dass
zumindest in gutre Näherung die obigen Forderugen nach Lage des Maximums und Glattheit erfüllt werden.
Nehmen wir an, der Algorithmus hätte das Spektrum 1, 3, und 9 für geeignet gehalten, dann müssen die Faktoren
f0 bis f2 und der Weissanteil w bestimmt werden, damit folgendes für den in
ein Spektrum umzurechnenden RGB-Wert gilt:
R = f0 ⋅ R1 + f1 ⋅ R3 + f2 ⋅ R9 + w
G = f0 ⋅ G1 + f1 ⋅ G3 + f2 ⋅ G9 + w
B = f0 ⋅ B1 + f1 ⋅ B3 + f2 ⋅ B9 + w
Die Auswahl der Teilspektren erfolg über eine Kette von if-Anweisungen, die Bestimmung der Faktoren gegebenfalls
durch ein paar Divisionen und Mulitplikationen.
Der weitere Vorteil der Linearzerlegung ist, dass man ein ganzes Bild in einem Rutsch in ein Spektrum zerlegen kann und dann
nicht n spektrale Intensitäten (die Anzahl der Wellenlängen, also so ca. 100) pro Pixel, sondern nur wenige Faktoren und wenige
Indizes speichern muss. Im konkreten Fall - so viel kann verrraten werden - sind das 9 Werte, also 9 "Kanäle" pro RGB-Wert.
Probleme der Linearkombinationen
Ganz klar, mit einer Linearkombinationen eines begrenzten Sets von Grundspektren können die obigen Forderungen
nach Lage des Maximums, der Glattheit usw. nur bedingt eingehalten werden. Da das Ziel aber kein physikalisch
richtiges Spektrum ist sondern nur "plausibel" sein soll, gelingt das eingentlich recht gut. Denn die eigentlich
wichtige Bedingung, dass die Addition des Spektrum wieder den ursprünglichen Pixelwert ergibt ist im Rahmen der
numerischen Genauigkeit gut erfüllt. Um den Wert zu nennen der Fehler ist unter 1%. Optisch nicht sichtbar, aber
bei Differenzbildung von originalen und prozessiertem Bild sichtbar.
Im folgenden Beispiel wurde jeder Pixel in ein Spektrum mit 89 Einzelwellenlängen umgerechnet und
schliessend diese Einzelwellenlänge auffsummiert. Keinerleich geometrische Transformation.
Die Abweichungen sind maximal ein Pixelwert also 1 / 255stel.



Abb. 7 spektrale Zerlegung und Aufsummieren des Spektrums
links oben: orginales Bild
rechts oben: prozessiertes Bild (Optorsion-Plugin ohne geometrishe Verzerrung)
unten: Differenz (ca. um Faktor 255 verstärt)
Schwieriger ist da schon das Problem, dass immer gewährleistet werden muss, dass ähnliche RGB-Werte auch ähnliche
Spektren ergeben müssen. Das Problem wurde gelöst, aber hier mal ein Beispiel des Optorsion-Plugins vor der Lösung
des Problems:




Abb. 8 Artefakte bei ungeeignetem Algorithmus zur Spektrumerstellung
links oben: verzerrtes Bild mit ganz einfachem Spektrum-Algorithmus
rechts oben: verzerrtes Bild vom Ausschnitt des Himmels (rechte Seite mit Gaussblur-Filter)
links unten: verzerrtes Bild mit ganz alten, noch nicht guten, Spektrum-Algorithmus
rechts unten: verzerrtes Bild mit gutem Algorithmus zur Spektrumerstellung
Man sieht deutlich die Artefakte, die entstehen, wenn die Spektrumerstellung nicht den
geforderten Anforderungen entspricht. Besonders schlimm am Himmel oben. Insbesondere auch, dass selbst geglättete Verläufe
bei wellenlängerabhängiger Verzerrung plötzlich Artefakte aufweisen können.
Der Algorithmus im Detail
Später...
Beispiele
Wie sieht nun ein Spektrum aus, das von einem RGB-Pixel erzeugt wurde?
Die ernüchternde Antwort ist: rabenschwarz! Und das ist auch logisch, denn die Helligkeit
eines Pixels wird über 100 oder mehr Pixel verschmiert. Die normale 8 bit reicht kaum
aus, um das richtig darzustellen. Der Effekt wirkt also erst im Gesamtbild wenn sich viel Pixel
addieren. Um folgenden Beispiel wurden die Spektren verstärkt um einen Eindruck davon zu gewinnen:
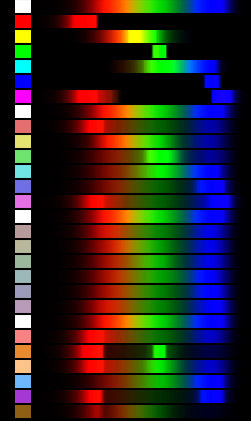
Abb. 8 Spektren (verstärkt um faktor 30) aus verschiedenen RGB-Werten
MAn sieht, dass die Spektrem der "reinen" Farben Rot, Grün und Blau sehr schmalbandig sind um kein Übersprechen
und damit Farbverfälschungen zu vermeiden. Die "Mischfarben" Gelb und Cyan sind dagegen schon breitbandiger.
Man beachte insbesondere Magenta. Hier sind sowohl rote als auch blaue Spektralanteile vorhanden aber zusätzlich
noch violette. Dabei ist das violett recht dunkel,aber man erkennt dass es weiter nach rechts geht als reines
Blau. Mit zunehmenden Weissanteil werden die Maxima der Spektren breitbändiger. Beim reinen Rot habe ich mir erlaubt
das Spektrum im roten Bereich noch zu verlängern.
Im nächsten Bild wurde das Bild mit dem Optorsion-Plugin in abhängigkeit von der Wellenlänge verschoben.
Man sieht, dass mit größerer Helligkeit das Spektrum auch realistischer aussieht.

Abb. 8 spektraler Effekt mit dem Optorsion-Plugin (das Spektrum wurde hier nicht verstärkt)
|
|

